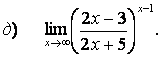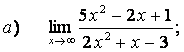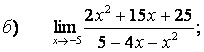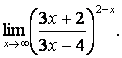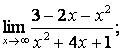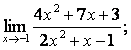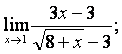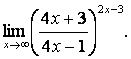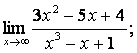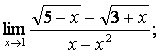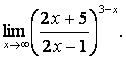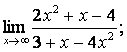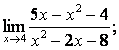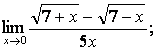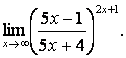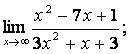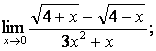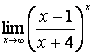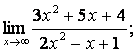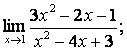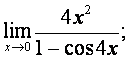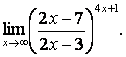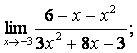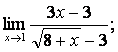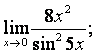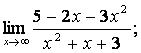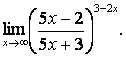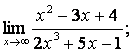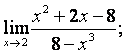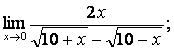Международный Институт XXI Века

�Высшая Математика�

Программа для студентов 1-го курса (1 и 2 сем.)

Преподаватель: Власов

Раздел 1.Аналитическая геометрия и линейная алгебра

Определители 2-го и n-го порядков.

Линейные операции над векторами. Линейная зависимость векторов. Скалярное, векторное и смешанное произведения векторов и их свойства. Геометрическое векторное линейное пространство.

Различные уравнения плоскости и прямой в пространстве. Взаимное расположение прямых и плоскостей в пространстве.

Матрицы. Линейные операции над матрицами. Определитель матрицы. Произведение матриц. Обратная матрица.

Системы линейных уравнений. Формулы Крамера. Матричный способ решения системы. Ранг матрицы. Теорема Кронекера �Капелли. Метод Гаусса. Нахождение общего решения систем линейных уравнений. Модель Леонтьева многоотраслевой экономики.

Линейное пространство. Базис и координаты.

Линейный оператор. Матрица линейного оператора. Собственные векторы и собственные значения линейного оператора.

Раздел 2.Введение в анализ

            Понятие функции. Множества, операции над множествами. Способы задания функций.

            Предел функции на бесконечности и в точке. Свойства пределов. Основные виды неопределенностей. Бесконечно малые и бесконечно большие функции.  Непрерывность функции в точке и на множестве. Точки разрыва и их классификация.

Раздел 3. Дифференциальное исчисление

            Производная и дифференциал первого порядка . Связь с  непрерывностью. Геометрический и физический смысл производной. Уравнение касательной к графику функции. Дифференцируемость функции. Таблица производных основных элементарных функций. Свойства производной. Производная сложной и обратной функции. Производные высших порядков. Правило Лопиталя. Формула Тейлора. Экономический смысл производной. Использование понятия производной в экономике. Экстремумы функции. Наибольшее и наименьшее значения функции на отрезке.  Построение графиков функций с помощью производных первого и второго порядков.

         Раздел 4. Функции многих переменных

            Основные понятия. Линии уровня.  Частные производные. Дифференцируемость функции двух переменных Производная по направлению. Градиент. Формула Тейлора. Экстремумы функции двух переменных. Условные экстремумы. Выпуклые функции двух переменных. Метод наименьших квадратов. Функции нескольких переменных в экономической теории.          

         Раздел 5. Интегральное исчисление

         Раздел 6. Дифференциальные уравнения.

Неопределенный интеграл. Таблица неопределенных интегралов.

Метод интегрирования по частям и замена переменной. Интегрирование различных классов функций.

            Определенный интеграл. Геометрический смысл. Основные свойства.

Производная интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница. Метод интегрирования по частям и замена переменной. Несобственные интегралы. Использование понятия определенного интеграла в экономике.

            Основные понятия. Дифференциальные уравнения первого порядка .Задача Коши. Элементы качественного анализа. Линейные дифференциальные уравнения первого порядка. Дифференциальные уравнения высшего порядка допускающие понижение порядка. Линейные дифференциальные уравнения с постоянными коэффициентами. Фундаментальная система решений. Метод подбора. Метод вариации произвольных постоянных. Использование дифференциальных уравнений в экономической динамике.

         Раздел 7. Ряды

            Основные понятия. Сходимость ряда. Достаточные признаки сходимости для положительных числовых рядов.

            Степенные ряды. Ряд Тейлора. Применение рядов в приближенных вычислениях.

         Литература

1.Красс М.С., Чупрынов Б.П. Математика для экономистов.-СПб.:Питер,2004.

2.Кремер Н.Ш., Путко Б.А. и др. Высшая математика для экономиств.-М.:Банки и биржи, ЮНИТИ, 1998.

3.Клетеник Д.В. Сборник задач по аналитической геометрии, М.,1972.

4.Кузнецов Л.А. Сборник заданий по высшей математике. М.Высшая школа.,1994.

            Лекции, 1 семестр ( 36 ч.)

1.Геометрические векторы. Линейные операции Проекции и координаты вектора. Разложение по базису. Линейные операции в координатной форме.

.Скалярное произведение двух векторов. Условие перпендикулярности. Свойства. Скалярное произведение в координатной форме.

2.Векторное произведение двух векторов. Свойства. Векторное произведение в координатной форме. Смешанное произведение трех векторов.

3.Уравнение плоскости, проходящей через заданную точку и имеющую заданный нормальный вектор. Общее уравнение плоскости.

4..Уравнение прямой в пространстве : канонические, параметрические, общие.

5.Матрицы .Линейные операции над матрицами . Умножение матриц. Обратная матрица.

6.Решение систем линейных уравнений. Правило Крамера. Метод Гаусса.

Ранг матрицы. Теорема Кронекера � Капелли.

7.Понятие о линейном пространстве. Линейно зависимые и линейно независимые системы векторов. Базис и размерность линейного пространства.

Однородные системы линейных уравнений. Пространство решений, его размерность. Структура общего решения.

            Неоднородные системы линейных уравнений. Структура общего решения.

8.Линейный оператор. Матрица линейного оператора. Собственные вектора и собственные значения линейного оператора.

9.Множества, операции над ними. Понятие функции. Способы её задания.

Предел функции на бесконечности.

10.Предел функции в точке .Бесконечно малые функции .Асимптотическое разложение функции, имеющей предел. Арифметические действия с пределами.

11. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые. Вычисление пределов с помощью эквивалентных бесконечно малых.

12.Непрерывность функции в точке и на промежутке. Точки разрыва и их классификация.

13.Понятие производной. Геометрический и физический смысл производной.

            Уравнение касательной и нормали к графику функции. Понятие дифференцируемости функции. Дифференциал. Таблица производных.

14.Производная сложной функции. Обратная функция. Дифференцирование обратной функции. Применение производной в экономике. Эластичность функции.

15.Производные высших порядков. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.

16. Условия возрастания и убывания функции в точке и на промежутке. Локальный экстремум. Направления выпуклости графика функции. Достаточные условия экстремума по первой  и второй производной. Наибольшее и наименьшее значения функции непрерывной на отрезке.

17.Асимптоты графика функции. Общая схема построения графика функции.

18. Формула Тейлора. Применение формулы Тейлора для локального исследования поведения функции.

Практические занятия(36ч.)

1.Определители 2-го и 3-го порядков. Миноры и алгебраические дополнения. Правило Крамера.

2.Геометрический вектор, его координаты, длина, направляющие косинусы. Линейные операции над векторами в координатной форме. Разложение вектора по базису. Коллинеарные векторы. Орт вектора.

3.Скалярное произведение векторов. Векторное произведение двух векторов.

Смешанное произведение трех векторов.

4.Уравнение плоскости. Уравнение прямой в пространстве.

5.Смешанные задачи на плоскость и прямую в пространстве.

6.Контрольная работа: �Аналитическая геометрия�.

7.Действия над матрицами. Обратная матрица. Матричный метод решения систем линейных уравнений.

8.Метод Гаусса исследования совместности и решения систем линейных уравнений. Однородная система линейных уравнений. Неоднородная система линейных уравнений. Структура общего решения.

9.Контрольная работа: �Линейная алгебра�.

10.Предел функции на бесконечности. Предел функции в точке. Простейшие приемы вычисления.

11.Вычисление пределов с помощью эквивалентных бесконечно малых.

12.Производные элементарных функций.

13.Дифференцирование сложной функции. Логарифмическое дифференцирование. Касательная и нормаль к кривой.

14.Производные высших порядков. Правило Лопиталя.

15.Контрольная работа: �Дифференцирование�.

16.Экстремумы функции. Направления выпуклости графика функции.

17.Асимптоты графика функции. Общая схема исследования функции.

18.Контрольная работа: �Графики�.

ПРИМЕРНЫЕ ВОПРОСЫ (нужна редакция)

1. Предел числовой последовательности.
2. Предел функции в точке и в бесконечности.
3. Бесконечно малые функции и их свойства.
4. Основные теоремы о пределах функции.
5. Первый и второй замечательные пределы, их следствия.
6. Сравнение бесконечно малых функций.
7. Неопределенные выражения. Приемы раскрытия неопределенных выражений.
8. Непрерывность функции в точке. Точки разрыва функции и их классификация.
9. Основные свойства функции, непрерывной в точке. Непрерывность функции на отрезке.
10. Производная. Определение, геометрический смысл.
11. Дифференциал. Определение, геометрический смысл.
12. Основные правила дифференцирования.
13. Таблица производных основных элементарных функций.
14. Правила дифференцирования сложной и неявной функций.
15. Производные высших порядков. Определение, правила нахождения.
16. Правило Лопиталя.
17. Основные теоремы дифференциального исчисления.
18. Возрастание и убывание функции. Определение, графическое представление.
19. Теоремы об условиях возрастания и убывания функции.
20. Экстремумы функции. Определения, необходимое условие существования экстремума.
21. Достаточные условия существования экстремума.
22. Наибольшее и наименьшее значение функции на отрезке.
23. Выпуклость функции. Определение, условия выпуклости функции.
24. Точки перегиба. Определение, условия существования.
25. Асимптоты графика функции. Определение, уравнения асимптот.
26. Схема исследования функции и построения ее графика.
27. Первообразная. Неопределенный интеграл. Основные понятия и определения.
28. Основные свойства неопределенного интеграла.
29. Основные методы интегрирования.
30. Таблица неопределенных интегралов от простейших функций.
31. Рациональные дроби. Основные понятия. Разложение рациональной дроби на простейшие.
32. Интегрирование простейших рациональных дробей.
33. Интегрирование тригонометрических выражений.
34. Интегрирование некоторых иррациональных функций.
35. Определенный интеграл. Определение, геометрический смысл.
36. Основные свойства определенного интеграла.
37. Вычисление определенного интеграла. Формула Ньютона-Лейбница.
38. Основные методы вычисления определенного интеграла.
39. Вычисление площади плоской криволинейной трапеции.
40. Вычисление длины дуги плоской кривой.
41. Вычисление объёма тела вращения.

ПРИМЕРЫ ЗАДАЧ

1.     Функции.

1.1.   Определить на какое множество функция  отображает множество (0; 1).

1.2.   Определить на какое множество функция  отображает множество  (0; 2).

2.     Пределы дробно-рациональных функций и замечательные пределы

Вычислить пределы:

.  .

3.     Сложные пределы

3.1.   .

3.2.  

4.     Дифференцируемость функции

4.1.   Вычислить по определению значение производной функции  в точке х₀=2.

5.     Производные элементарных функций

5.1.   Найти производную функции .

6.     Геометрический смысл производной. Уравнение касательной

6.1.   Составить уравнение касательной к графику функции  в точке (1;2).

7.     Возрастание, убывание, экстремумы функции одной переменной.

7.1.   Исследовать на экстремум функцию   y=2x²+6x-7.

7.2.   Определить наибольшее и наименьшее значение функции  на отрезке .

8.     Выпуклость, вогнутость, точки перегиба функции одной переменной

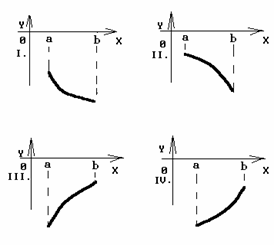
8.1.   График какой функции на всем отрезке  одновременно удовлетворяет трем условиям: ; ; ?

8.2.   Исследовать характер вогнутости функции  на отрезке  .

9.     Табличные интегралы

9.1.   Вычислить интеграл.

10.           Интегрирование подстановкой

10.1.                   Вычислить интеграл .

11.           Интегрирование по частям

11.1.                      Вычислить интеграл .

12.           Геометрический смысл интеграла

12.1.                   Каким интегралом задается  лощадь заштрихованной части фигуры, изображенной на чертеже?

рекомендуемая литература

Основная:

1.      Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. � 2-е изд. � М.: Айрис-пресс, 2004. -608 с.: ил. �(Высшее образование).

2.      Зимина О.В., Кириллов А.И., Сальников Т.А. Высшая математика / под ред. А.И. Кириллова. � 3-е изд., испр. � М.: ФИЗМАТЛИТ, 2003. � 368 с. � (Решебник) � ISBN 5-9221-0441-1.

3.      Кремер Н.Ш. и др.Высшая математика для экономистов. Учебник, ЮНИТИ, М.,2002г.

4.      Щипачев В.С. Задачи по высшей математике. учебное пособие. Высшая школа, М.,1997.

Дополнительная:

1.      Рудык Б.М. и др.Общий курс высшей математики для экономистов. учебник, ИНФРА-М, М.,2000г.

2.      Солодовников А.С. и др. Математика в экономике. часть 1,2,3. учебник,�финансы и статистика�, М.,2000-2001г.г.

3.      Красс М.С.,Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании (учебник для экономистов ). Дело,М.,2001.

4.      Малыхин В.И. Математика в экономике. (учебное пособие ).ИНФРА-М.М.,2002.

5.      Ермаков В.И. Сборник задач по высшей математике для экономистов (учебное пособие ) ИНФРА-М.М.,2002.

6.      Пискунов Н.С. Дифференциальное исчисление для втузов. В2-х томах, Наука, М.,(издание стереотипное ).

7.      Данко П.Е. и др. Высшая математика в упражнениях и задачах. В 2-х томах.Высшая школа, М.,1997.

8.      Берман Г.Н.Сборник задач по курсу математического анализа (учебное пособие ) Изд. стереотип.2002.

I. Найти пределы функций, не пользуясь правилом Лопиталя.

II. Задана функция y=f(x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.

III. Найти производные  следующих функций.

IV.            Найти пределы функции, применяя правило Лопиталя.

V. Методами дифференциального исчисления исследовать функцию y = f(x) и по результатам исследования построить ее график. Найти наименьшее и наибольшее значения функции на заданном отрезке.

VI. Найти неопределенные интегралы. В заданиях а), б), в) результат проверить дифференцированием.

VII. Вычислить определенные интегралы.